
Year Three - Tiling to Understand Area
Home - Tiling to Understand Area Map
About this Big Idea
In this Big Idea students explore area through tiling visualisations so as to develop a deep understanding of this fundamental mathematical concept.
Understanding Goals:
Students will understand:
- the concept of area and its relationship to two-dimensional space.
- why different shapes might have the same area.
- the distinction between perimeter and area.
- how creativity and innovation are essential parts of mathematics.
Background:
It is important that students have a clear understanding of the distinction between perimeter and area. 'Perimeter' is derived from the Greek words that mean to measure around the outside: peri, meaning 'around', and metron, meaning 'measure'. Area relates to the measurement of two-dimensional space in the same way that volume and capacity relate to the measurement of three-dimensional space.
Core Content from the Syllabus:
Working Mathematically
Area
- estimate the areas of rectangles (including squares) in square centimetres
- discuss strategies used to estimate area in square centimetres, eg visualising repeated units (Communicating, Problem Solving)
- compare the areas of regular and irregular shapes by informal means
- measure the areas of irregular shapes using a square-centimetre grid overlay
- compare how different placements of a grid overlay make measuring area easier or harder (Problem Solving)
- explain why two students may obtain different measurements of the area of the same irregular shape (Communicating, Reasoning)
Language:
- length, distance, metre, centimetre, millimetre, ruler, measure, estimate, perimeter
- area, irregular area, measure, grid, row, column, parts of (units), square centimetre, square metre
Connected to:
Mindset Mathematics Learning Activities

Visualise
Students use geoboards and square tiles to develop an understanding of area as covering with square units. Students make shapes on the geoboard to figure out, "How big is this shape?"- See page 101
Questions for reflection:
- What shapes did you make?
- How did you figure out how much space the shape takes up?
- How did you record your thinking?
- What is area? Provide examples to show what area is?
- Can you distinguish between perimeter and area?

Play
Students play with area by building pixelated letters out of square units to see what letters could have an area of 4, 5, 6 and up to 12 square units. - See page 111

Questions for reflection:
- What area can make the most letters? Why?
- What letters can be made with many different areas? Why?
- Were there any letters that you couldn't make? Why?
- Do you think you have found all the possible letters that can be made with these areas? Why or Why not?
- If you were to make the digits 0-9 on a grid, which digit do you think would have the greatest area? The least? Why?
Digital Technology Extension
Students can apply their knowledge of letter area and designs to the challenge of displaying letters on small LED displays such as that on the BBC MicroBit. Students will need to use their knowledge of the area required for each letter and translate this to the 5 x 5 grid of LED's on the MicroBit or similar display.
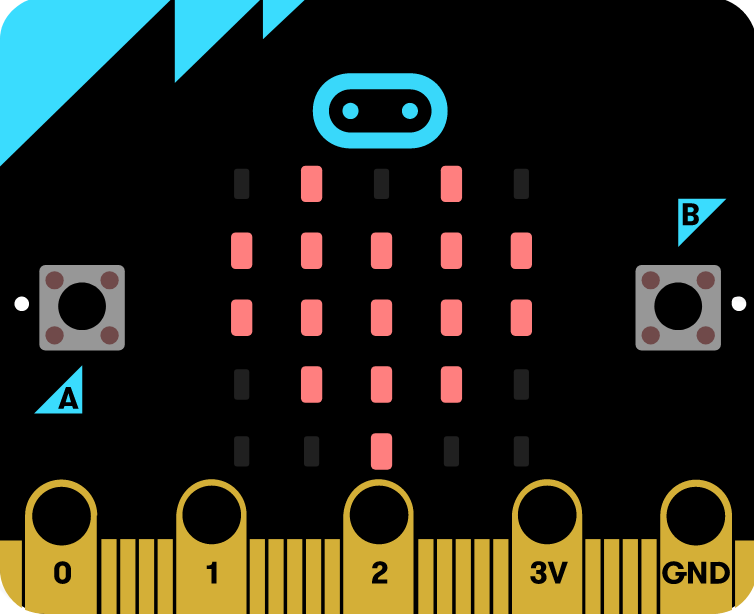
Image - BBC MicroBit - an easily programmed system on a chip computer with LED display.
Design & Production Extension
Students could investigate how a display board could be made using coloured paper, cardboard and craft supplies. Students would need to consider the size of the matrix they would need to display all letters and numbers and devise a method for changing the display by perhaps flipping pixels over or covering unused pixels. Displays could be back lit by placing on a light box or by attaching to a window.

Investigate
Students create rectangles with the same area and look for patterns opening the door to connecting area and multiplication. - See page 119
Questions for reflection:
- What evidence did we find regarding our conjectures? What support did we find?
- What ideas need revision?
- What other evidence might we need to gather?
- What patterns do you notice?
- What new questions do you have?
- What did you notice in the rectangles that surprised you? What are you wondering now?
Credit:
Boaler, Munson & Williams (2018) - Mindset Mathematics: Visualizing and investigating big ideas Grade 5
NESA - Mathematics K-10 - 2012







