

Home - Being Flexible With Number Map
In this Big Idea students are invited to think visually and creatively about numbers. In place of memorising number facts, students develop an understanding of the relationships between and within numbers as they represent them in multiple forms and engage in 'number talks' with teachers and peers.
"Fluency has nothing to do with speed; students who are fluent with numbers are those who are comfortable with numbers, which rarely comes about when mathematics is associated with speed." (Boaler, Munson & Williams. 2018)
Read more about the negative impact of memorisation without understanding here - Fluency Without Fear
I was always deeply uncertain about my own intellectual capacity; I thought I was unintelligent. And it is true that I was, and still am, rather slow. I need time to seize things because I always need to understand them fully. Towards the end of the eleventh grade, I secretly thought of myself as stupid. I worried about this for a long time.
I'm still just as slow… At the end of the eleventh grade, I took the measure of the situation, and came to the conclusion that rapidity doesn't have a precise relation to intelligence. What is important is to deeply understand things and their relations to each other. This is where intelligence lies. The fact of being quick or slow isn't really relevant.
(Laurent Schwartz, 2001) (Fields Medallist, 1950 - The Fields Medal is regarded as one of the highest honors a mathematician can receive.)
Students will understand:
In Stage 2, the emphasis in multiplication and division is on students developing mental strategies and using their own (informal) methods for recording their strategies. Comparing their own method of solution with the methods of other students will lead to the identification of efficient mental and written strategies. One problem may have several acceptable methods of solution.
When beginning to build and read multiplication facts aloud, it is best to use a language pattern of words that relates back to concrete materials such as arrays.
Linking multiplication and division is an important understanding for students in Stage 2. They should come to realise that division 'undoes' multiplication and multiplication 'undoes' division.
Whole Number
Multiplication & Division

Students build flexibility with multiplicative thinking by creating arrays and developing creative ways of seeing how many the array represents. - See page 211
Questions for reflection:

Students build flexibility with multiplication through the area game "How close to 100?". - See page 217
Questions for reflection:

Students create growing patterns with rectangles and then locate those rectangles on the multiplication table and see what new patterns this reveals. - See page 222
Questions for reflection:

In this inquiry students explore odd and even numbers and in doing so develop a deep understanding of the concept. As they investigate these important categories in number they will develop their understanding of mathematical thinking as they attempt to prove ideas that they may have taken for granted. This 'Beyond' was inspired by "Yes, but Why?: Teaching for understanding in mathematics" by Ed Southall.
Patterns & Algebra
What does it mean to generalise?
According to The Australian Association of Mathematics Teachers, "eventually students need to learn that these concepts and procedures are general — that is, that they apply to a wide variety of different situations including ones they have not yet encountered. In other words, teaching should aim to encourage students to make abstractions and generalisations. . . .For example, students may notice that the numbers in a growing pattern increase by two each time. This is an example of a generalisation — a relationship that is always true."
In this inquiry students are required to make a generalisation about a pattern that they know well; odd and even numbers. By Year Three students have no doubt encountered the concept of 'odd & even' and know which numbers belong to each set, but they have probably never been asked to show proof of their knowledge. Students will also explore some of the interesting patterns which occur when we add or multiply with odd and even numbers and make generalisations from their observations.

Students begin by exploring visualisations of numbers that they know well. By arranging counters or blocks into arrays students explore the patterns that are or are not possible with particular numbers between one and twenty. It may help to ask students to put aside their prior knowledge of number patterns to focus on the visualisations that they can construct through experimentation.
Example Arrays:

The arrays above show how the numbers one, three & five do not organise neatly into two rows. What does this reveal about these numbers?

The arrays above show how the numbers two, four, six and eight organise neatly into two rows. What does this reveal about these numbers?



The arrays above contrast the properties of four, five and nine. Four and nine can be arranged into a square. Five can not be arranged in any other way without having a 'loose end'. What does this reveal about these numbers?
Students should notice that:
Questions for reflection:
Look Fors:
Students should notice that some numbers can not be organised into two row arrays, they make odd shapes when we try to do so. Even numbers can be organised into two row arrays with each row even in length.
Students might notice that some numbers can only be organised into a single row if they are to have no loose ends (3, 5, 7, 11, 13, 17, 19). Students should see that there is something unique about these numbers. Some may know that we call these numbers 'Prime Numbers'. You should relate this discussion to the Play and Investigate activities above.

Having learned something about odd and even numbers, students now use visualisation strategies to explore what happens when we add or multiply different combinations of odd and even numbers. We will construct visualisations that offer insights for the following questions:
Example Arrays:

Array One - 2 + 3 = 5 - Adding and even and an odd produces an array with a loose end, an odd number.

Array Two - 2 + 4 = 6 - Adding an even and an even produces an array without a loose end, an even number.

Array Three - 3 x 2 = 6 - Multiplying an odd by an even produces an array without a loose end, an even number.

Array Four - 3 x 3 = 9 - Multiplying an odd by an odd produces an array with a loose end, an odd number.
Questions for Reflection:

In this game students develop a better understanding of the effect of multiplying different combinations of odd and even numbers. Students should see quite quickly that this is an unfair game and the choice to play 'Evens' is a winning move.
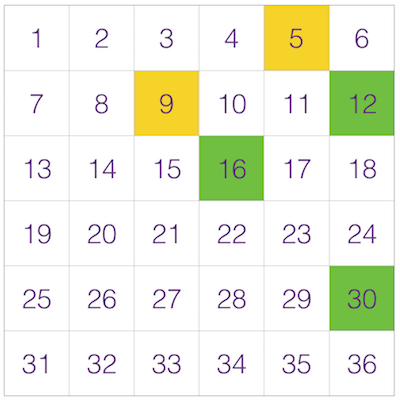
Player one (Green) is playing for evens. They rolled the following combinations - (6 & 2), (4 & 4), (5 & 6). They also rolled (5 & 5) so one roll was wasted.
Player two (Yellow) is playing for odds. They rolled the following combinations - (5 & 1), (3 & 3). They also rolled (6 & 1), (4 & 2) so two rolls were wasted.
Questions for reflection:
Going further:
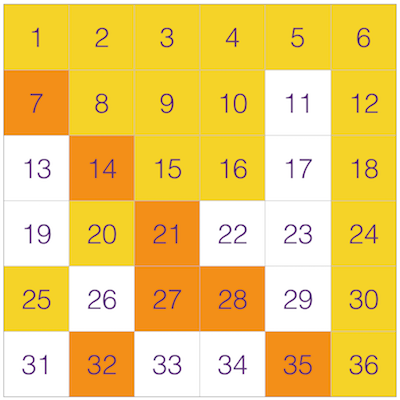
Yellow numbers can be rolled using two six sided dice. Orange numbers are made possible with a ten sided dice. Notice that eight odd numbers can not be rolled at all.
Look fors:
What are students thinking? - Beyond the game is the thinking that it encourages. This is a good opportunity for an extended ‘Number Talk’ and a thinking routine such as ‘Peel the Fruit’ might be ideal to make the thinking of the students visible. Students might think that there are more even numbers than odd; a false assumption. A sound understanding here will require students to see a pattern linked to multiplying by an even number. This is a pattern that can be made more obvious by constructing a table to show possible values from multiplication or by colour coding numbers on a grid.

In this investigation students explore why some of the numbers in the previous activities were very inflexible or impossible to achieve. They will also investigate why some numbers form a square array while others do not. In mathematical language this involves investigating Primes and Square Numbers. Students will use Cuisenaire blocks to physically model the factors of various numbers. In the post investigation discussion the terms Prime and Square Number can be introduced.
This is intended as an introduction to Prime and Square Numbers. Students return to these concepts in Stage Three and have fun exploring their properties in greater detail then.
Cuisenaire rods are an excellent resource for exploring a range of mathematical concepts. In this instance we will let the small white block "represent" one and thus the large orange block represents ten. Multiple blocks can then be arranged on top of a selected block to model its factors as shown below. When modeling simple multiplication, only blocks of the same colour can be used in a row.

The first arrangement uses the light green block to represent three. On top of this it can be seen that three white blocks representing 3 x 1 = 3 can be placed on top. There is no other arrangement of like-sized blocks that cover the three-block.
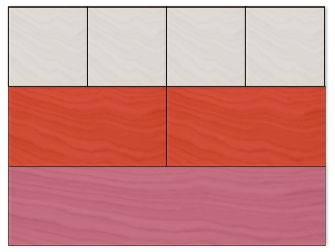

Here the pink bloc represents four and it is shown that two red blocks (2 x 2 = 4) and four white blocks (4 x 1 = 4). In the second image the yellow block represents five (and 1 x 5 = 5), it can only be covered in white blocks (5 x 1 = 5). Students should be encouraged to group together numbers which can only be covered in white blocks. When students start to notice patterns like this and group numbers together by the properties they observe they are using the mathematical thinking move of 'categorisation'.
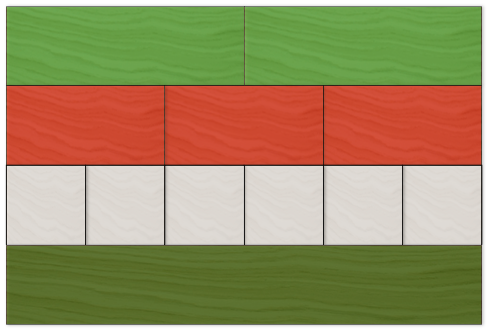
In this image the dark green block represents six. The white blocks reveal that 6 x 1 = 6. The red blocks reveal that 3 x 2 = 6. The light green blocks reveal that 2 x 3 = 6. Students should notice that the top two rows show multiplication of the same numbers and proof of the commutative property of multiplication i.e. 3 x 2 = 2 x 3 Students should also notice that the dark green rod in this case represents 1 x 6 = 6.
Identifying Primes
A prime is a number that has exactly two factors, this explains why two is prime and one is not (it has only one factor, zero is another special case). Five is prime because it has two factors, five and one. So too is three as shown above. When we represent a prime with cuisenaire rods we find that it can only be covered with white blocks, they can not be evenly divided into any other whole number. This is also why some numbers were not possible in the dice game above. Only primes smaller than six if using two six sided dice, or ten if using two ten sided dice could be rolled. Once students start to find numbers which can only be covered in white cubes they can be encouraged to find others. Numbers which are larger than 10 can be represented by adding blocks together but you must be clear that in these cases you are using addition to make a large number e.g. orange (10) plus black (7) represent 17.
Questions for reflection:
Exploring Square Numbers
When visualising numbers in arrays students may have noticed that some numbers can be arranged into a square, while others can't. These numbers are square numbers, a special category. Square numbers are formed when one number is multiplied by itself, e.g. 3 x 3 produces the square number 9.
Students can explore square numbers using cuisenaire blocks. They should see that with square numbers they can arrange the blocks (other than the single block used to represent the number) in a square shape as below:



The pink rod represents four. The red blocks each represent two, we can see that 2 x 2 = 4 or (22 = 4) and that a square can be formed. Using white blocks we see that we can arrange four blocks to form a square. By contrast, five white blocks can not be used to form a square. Six is also not square as demonstrated. Students should explore what numbers can be arranged into a square. It may be necessary to review what a square is and is not.
Questions for reflection:
Use of the word represent to describe the relationship between any given Cuisenaire Rod and a number is very deliberate. Depending on context the rods 'represent' different numbers or fractions and if it was said that 'it is' a number of equals a number students may be rightly confused. In place of saying that the light green rod equals or is three, we choose to say it 'represents' three (or another number as relevant). Students need to be shown that the rod represents a number based upon its relationship to the number we choose to have represent one. The examples below demonstrate how this changes:
In the first example the white block is representing one. In this case the light green block represent three. If the light green block was representing one in this case, the white block would be 1⁄3.


In this example the dark green block is representing one. The light green block now represents 1⁄2. In the final example the dark blue block represent one and the light green block now represents 1⁄3.
Students may also be confused when they are asked to see not a one to one correspondence where one block represents one, but where the size of the block and its relationship to other blocks matters.
