

Home - Finding & Using Unit Rates Map
In this Big Idea students explore the concept of Unit Rates as it apples to situations where we are buying items in bulk or where we are interested in multiples of an item such as may occur in architecture, nature and biology. Students will understand how unit rates can be used to allow us to compare the value or scale of differing quantities in ways that are comparable. This is also an excellent opportunity for students to refine their understanding of multiplication and division. Students will enjoy applying their mathematical thinking to real world financial situations.
Students will understand:
Students should have an understanding that an inverse operation is an operation that reverses the effect of the original operation. Addition and subtraction are inverse operations; multiplication and division are inverse operations. Students benefit from having an understanding of the effect that multiplication and division have on numbers, but will expand that understanding through this unit.
The simplest multiplication word problems relate to rates, e.g. 'If four students earn $3 each, how much do they have all together?' Another type of problem is related to ratio and uses language such as 'twice as many as' and 'six times as many as'.
Multiplication and Division

Students visualise the concept of unit rates by exploring tiling patterns that repeat infinitely across space so as to develop their understanding of the concept involved here before thinking about unit rates as numerical relationships. This requires students to identify the 'base unit' within a tiling pattern, i.e. the object within the pattern which repeats and is foundational to the spread of the pattern across the space. - See page 119

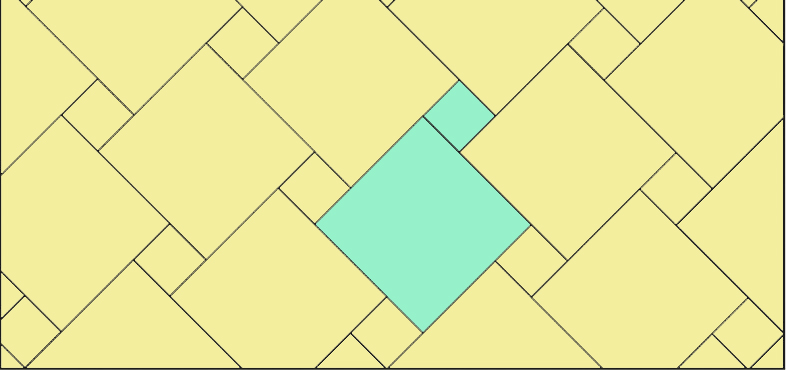
Questions for reflection:
As students make patterns of their own and share these with their peers, ask:

Students explore the diverse tiling patterns which are created by world cultures and discuss what these patterns reveal about the cultures that create them. As students explore these rich and varied patterns they continue their search for unit rates and 'base units'. Students will have opportunities to investigate the nature of tessellating patterns and expand their mathematical vocabulary. This exploration should help students to see the beauty of mathematics and that mathematics and patterns are a language with meaning and deep links to our cultural identity.
Questions for reflection:
There are many sources for inspiring and beautiful tiling patterns. A search of google images will reveal numerous options and by adding modifiers such as 'Islam', 'Celtic' or 'Ancient' a more refined set of results will be found. Students may be able to find interesting tiling patterns in the real world and churches and large public buildings often hold interesting examples. There are a many books which describe tiling patterns in detail and provide images and background information:




What's the best deal? Using this frequently asked question, students explore how to use rates to make comparisons while playing a shopping game at stations they create. An important part of this activity is the development of a visual proof for the deals that are offered. Students amy want to move very quickly towards numerical proofs but do so without and understanding of why their methods work. An essential element of mathematical thinking is being able to demonstrate, in multiple ways why a method works or a conclusion is valid. - See page 128
“We use representational forms to communicate ideas and as tools for reasoning. Therefore, mathematical proficiency hinges on learning how to construct, communicate, and reason with representations." (Selling. 2016 p191)
Questions for reflection:

How fast do you walk? Students collect data and develop ways of expressing speed to explore speed as a unit rate. In this activity students are required to consider unit rates in a familiar situation but one that they may not normally associate it with. An important aspect of this activity is the justification for the choices that students make around the units they use and how they combine these. - See page 136
Questions for reflection:
