

Home - Expanding the Number Line Map
In this Big Idea students explore numbers on a number line either side of zero using symmetry to help them understand the relative location of positive and negative numbers. Students benefit from developing a conceptual and visual understanding of negative numbers and research shows that revealing to students the symmetry of positive and negative numbers assist with this understanding and sound preparation for algebra. Moving too quickly to operations with negative numbers before students develop a sound understanding of their position on a number line relative to positive numbers which they know well inhibits latter learning as the foundation required is missing or weak.
Students will understand:
By Stage Three students should have had extensive experience with the number line and made use of it in a range of situations while counting and performing operations. In Stage Three this experience needs to continue to the left of zero and students need to extend their understanding of the number line into negative integers. Students will benefit from learning that the knowledge they have of positive integers will help them to understand negative integers and this unit should demystify numbers less than zero.
Note - In Year Five students "Explored the Coordinate Plane" without developing an understanding of negative numbers. This prior experience should benefit their learning in this Big Idea.
Whole Number
Patterns & Algebra

Students construct and explore number lines by folding adding machine tape to build understanding of negative integers through symmetry. - See page 94
Questions for reflection:

Students play "Number Line Bounce", building connections among integers on the number line, and addition and subtraction. - See page 101
Note: On the surface this may seem like a simple game and students may appear to have mastered the concepts involved. It is important and highly valuable to have students describe their thinking as this offers insights into how they are approaching the moves and will be relevant later. The "Look-Fors" on pages 104 & 105 should be referred to for guidance.
Questions for reflection:

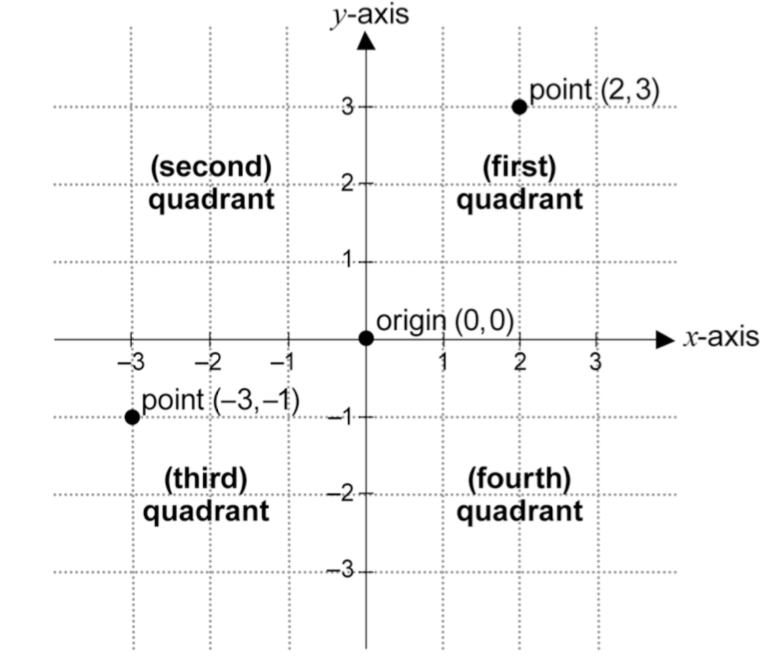
Students investigate lines on a coordinate plane (Cartesian Plane) and look for patterns in the integer ordered pairs of the points on those lines. Students build connections between the integers on the number line and the two number lines that make the coordinate plane. - See page 107
Questions for reflection:


Above & Below
Students will deepen their understanding of the expanded number line by visualising negative and positive integers in the real world. In this Visualise activity students collectively construct a number line to compare the relative height above or below sea level of significant landmarks. Students will need to collect information from a range of resources including maps and the internet to determine heights above and below sea level. Once this information is collected students will need to work collaboratively to construct a vertical number line that makes their knowledge visible.
Students will enjoy opportunities to create highly visual number lines that combine images and their artistic flair with their mathematical thinking. The number lines that students create in this way can be an affirmation of mathematics as a beautiful and visual discipline that helps us see our world in new ways.
Questions for reflection:

Warm & Cold
An important use of negative integers occurs in the centigrade scale for temperature. In this scale the "triple point of water" or more commonly the freezing point of water at sea level is defined as 0℃. Temperatures less than this are indicated with negative integers and students can enrich their understanding of negative integers by exploring and visualising temperatures.
In a manner similar to Visualise Part One (above) students create a visual representation using a number line of places and objects which are either very warm or very cold. Students can compare the temperature of places they may have visited with other known places on the Earths surface and then expand their inquiry as the look for places which are warmer of colder than those they have already discovered. Students can then expand their exploration further by including very cold objects e.g. liquid nitrogen at -195.8℃ or very hot e.g. iron which melts at 1510℃. Students might be interested in exploring the meaning of "absolute zero" which occurs at -273.15℃ and they are likely to be challenged by the idea that there can be no temperature less than this. The scientifically minded class might like to explore the Kelvin scale and students from United States of America may wish to share their knowledge of the Fahrenheit scale.
Questions for reflection:
Going further
As students explore the temperature of places around the world they are likely to also explore changes in temperature over time and make connections with what they know about Climate Change and Global Warming. This is particularly likely given the recent heat wave conditions across Australia. This visualisation and others like it show a pattern of temperature anomalies that students might like to discuss. It shows temperature anomalies in increments above and below normal with those which are below normal indicated with negative integers which introduces students to another way that we can use directed number or negative integers.
Questions for reflection:

Where in the world am I?
Students use information from their visualisations of world temperatures and altitudes to develop a class game of trivia. The game is designed to increase engagement with the visualisations and build familiarity with the information before students move to the Investigate activities below. Students will need to use a combination of data points to ensure that their location is unique but not immediately obvious e.g. I am at an altitude of 3776m and the temperature is -41℃, where am I?
Questions for reflection:
Working with large numbers and abbreviations
As students gather information for their visualisations they are likely to encounter some large numbers and possibly the abbreviation K for 1000 or multiples thereof. This is an excellent opportunity to discuss and review how this abbreviation is used e.g. 40K meaning 40,000. The class can discuss why such abbreviations might be used. This can also be a time to discuss rounding and approximations. Students might like to discuss the importance of accuracy and situations where it is less important. Is it OK to say that Mount Fuji in Japan is almost 4000m? Would it be OK to say 3800m? (The actual height is 3776m) Why or why not?

The Biggest Change
In this Investigation students use the information they have gathered for the two Visualisation activities and their knowledge of adding and subtracting negative and positive integers developed in the Play activity to discover the biggest change possible. Student will explore the relative height above or below sea level or temperature of the data points they have gathered, As they engage in this extended mathematical exploration students will encounter interesting correlations between data points e.g. a decrease in temperature with an increase in altitude.
Students should be encouraged to revisit the strategies that they found useful when playing "Number Line Bounce" and discuss how they can use their knowledge of the number line to check their mathematics e.g. If I start beneath sea level at -130m I have to climb 130m to reach sea level and then add another 220m to reach my final height above sea level of 220m that means a change of 130 + 220 or 350m. Students should be encouraged to make their thinking visible as a check that they are understanding the expanded number line.
Questions for reflection:
Look-Fors:
Are students showing an understanding of the symmetry between negative and positive integers? - Some students when they come to compare negative and positive integers will make the mistake of ignoring the distance that each number is from zero. A student doing this will calculate the difference between -130 and 220 as 90 rather than 350. Students who are making this error should be directed back to visualisation with the number line. As students build an understanding it is sufficient for number lines to be constructed quickly as a rough symbolic representation of the numbers involved. This allows students to visualise the numbers involved while demonstrating and building their ability to work with estimates and approximations of the real values involved.

The visualisation above shows a student who is decomposing the question into two parts; the distance to zero and the distance from there to the positive integer. Alternatively the student could be working with subtraction and decomposing from 220 to zero and then from zero to 130. Students might do this but still arrive at an incorrect solution revealing that when they approach the second step they do not add the distance to negative integer but subtract it. In both instances it is telling to have the student describe their thinking.
Are students confused when working only with negative integers? - Students might find the concept of subtracting a negative number from another negative number confusing. Some might treat one of the numbers as though it is positive and decide that the distance between the numbers is much greater. These students need to create a visualisation on a number line of the mathematics involved. Doing so should allow them to better see the relative location of the two numbers they are working with and for them to also see that it is the distance between them and not their distance from zero that is most relevant.
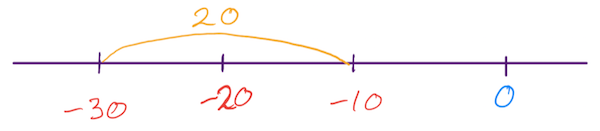
Generating Questions
This investigation can be extended by students developing and answering questions that emerge from the data. Students might ask which country in the world would I travel to if I wanted to experience the greatest extremes of temperature or the largest change in altitude, which country is the flattest, the deepest or highest, the hottest or coldest.
Students can be given time to develop Infographics that share their information with an audience. Infographics are introduced in Year Three where students read the book 'Animals by the Numbers' and students might like to revisit their thinking from this point in their learning. See Year Three "Solving Problems with Data"
